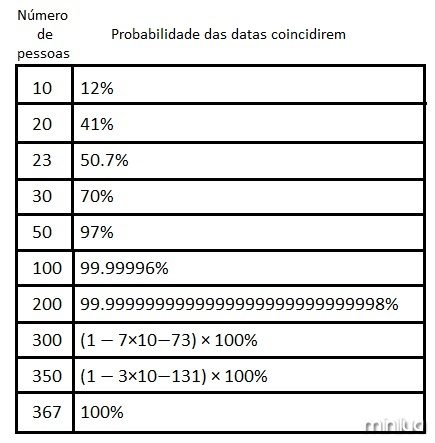
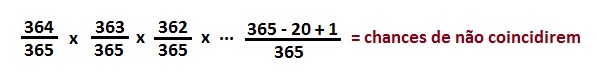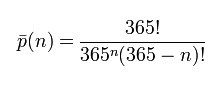O paradoxo do aniversário é um resultado incrível da teoria das probabilidades. Ele afirma que para um grupo de 23 (ou mais) pessoas escolhidas aleatoriamente, a chance de que duas pessoas farão aniversário no mesmo dia é de mais de 50%. Em uma festa com 30 pessoas, a probabilidade de haverem duas pessoas com a mesma data de aniversário é maior que 70%. Para um grupo de 57 ou mais pessoas, a probabilidade é maior do que 99%. Claro que ela não pode ser exatamente 100%, exceto que se tenha pelo menos 367 pessoas.
Isso nos parece muito surpreendente, porque acabamos comparando a data o nosso aniversários diretamente com os outros, mas essa não é a lógica por trás desta teoria.
O que acontece é o seguinte: Quando conhecemos uma pessoa e perguntarmos sua data de aniversário, a probabilidade de as datas de aniversário se coincidirem é de apenas 1 para 365 (1/365) ou seja 0,27%. Sendo assim, a probabilidade de você e seu novo amigo fazerem aniversário no mesmo dia é extremamente baixa. Mesmo que você pergunte a 20 pessoas, a probabilidade é de 20 pra 365, cerca de 5%, ou seja, ainda é baixa. Por isso, pensamos que é muito raro encontrar alguém que faça aniversário no mesmo dia que nós.
Só que não é assim que devemos calcular. A probabilidade neste caso deve ser pensada da seguinte forma: imagine que há 20 pessoas em uma sala, o que muda é o fato que cada uma dessas 20 pessoas fará a pergunta para as outras 19. Desta forma, cada pessoa tem uma pequena probabilidade de sucesso (que é de cerca de 5%), mas cada uma está tentando 19 vezes. Aumentando exponencialmente essa pequena probabilidade.
A maneira exata de analisar é a seguinte: digamos que você tenha um calendário na parede com os 365 dias do ano (desconsiderando o ano bissexto). Você marca um X no dia do seu aniversário. A pessoa seguinte terá apenas 364 dias em aberto disponíveis, portanto, a probabilidade das duas datas não colidirem é de 364/365, ou 99,7 %. A pessoa a seguir tem apenas 363 dias em aberto, o que reduz a probabilidade das datas não colidirem a 363/365, ou 99,4% e assim por diante até chegar na vigésima pessoa que terá 346 dias em aberto. No final, nós temos que multiplicar as probabilidades das datas de aniversários de todas as 20 pessoas não coincidirem. Essa multiplicação se dá justamente porque cada uma das 20 pessoas tenta 19 vezes. Então temos:
Caso você queira tentar, a fórmula para calcular é
Onde n é o número de pessoas no grupo. Então, da próxima vez em que estiver em um grupo grande de pessoas, faça o teste!